この記事では、c++において正規分布（ガウス分布）に従う乱数を発生させる方法について記述していきます。

一様分布の乱数（例えば、0~1の間の値を発生させる乱数）は情報の授業などで目にすることも多いのではないでしょうか。

移動ロボットの世界では、センサからの情報を正規分布（ガウス分布）に従うノイズを伴った情報として近似することがよくあります。
そこで今回は、正規分布（ガウス分布）に従う乱数を発生させる手法を備忘録も兼ねて書き留めていこうと思います。

参考 : ガウス分布のグラフの概形を確認する

サンプルコード

以下のコードは、平均0.0、標準偏差1.0の正規分布に従う乱数を発生させるサンプルコードとなっています。

正規分布に従う乱数はrandomというヘッダファイルをインクルードすると使用できるようになります。

正しく動作しているかを確認するために、正規分布に従う乱数を1000000回生成して、各値が何回出現しているかをグラフ化しています。

※グラフの描画にはにはmatplotlib-cppというライブラリを用いています。
matplotlib-cppの使い方はこちらを参考にしてみてください。

c++でmatplotlibを使う | MY ROBOTICS

#include <random>
#include <matplotlibcpp.h>

namespace plt = matplotlibcpp;

int main() {

	std::random_device seed;
	std::mt19937 engine(seed());            // メルセンヌ・ツイスター法
	// std::minstd_rand0 engine(seed());    // 線形合同法
	// std::ranlux24_base engine(seed());   // キャリー付き減算法

	double mu = 0.0, sig = 1.0;
	std::normal_distribution<> dist(mu, sig);

	int n = 1000000;
	std::vector<double> list(n);

	for (int i=0; i<n; ++i) {
		list[i] = dist(engine);
	}

	// 小領域に区切って、その中の乱数の個数を数える
	std::vector<double> numbers, x;
	double range = mu + sig * 5.0;
	double step = 0.1;

	for (double i=-range; i<=range; i+=step) {
		int number = 0;
		for (auto& el : list) {
			if (i-step/2.0 < el && el <= i+step/2.0) {
				++number;
			}
		}
		x.push_back(i);
		numbers.push_back(number);
	}

	plt::plot(x, numbers);
	plt::show();
}

#include <random>
#include <matplotlibcpp.h>

namespace plt = matplotlibcpp;


int main() {
    std::random_device seed;
    std::mt19937 engine(seed());            // メルセンヌ・ツイスター法
    // std::minstd_rand0 engine(seed());    // 線形合同法
    // std::ranlux24_base engine(seed());   // キャリー付き減算法

    double mu = 0.0, sig = 1.0;
    std::normal_distribution<> dist(mu, sig); 

    int n = 1000000;
    std::vector<double> list(n);

    for (int i=0; i<n; ++i) {
        list[i] = dist(engine);
    }

    // 小領域に区切って、その中の乱数の個数を数える
    std::vector<double> numbers, x;
    double range = mu + sig * 5.0;
    double step = 0.1;

    for (double i=-range; i<=range; i+=step) {
        int number = 0;
        for (auto& el : list) {
            if (i-step/2.0 < el && el <= i+step/2.0) {
                ++number;
            }
        }
        x.push_back(i);
        numbers.push_back(number);
    }

    plt::plot(x, numbers);
    plt::show();
}

コードの解説

擬似乱数を生成する

std::random_device seed;
std::mt19937 engine(seed());            // メルセンヌ・ツイスター法
// std::minstd_rand0 engine(seed());    // 線形合同法
// std::ranlux24_base engine(seed());   // キャリー付き減算法

1行目で乱数のタネとなる乱数シードを生成するクラスのインスタンスを生成。
2行目では乱数シードから決定的な乱数を生成するクラスの初期化を行っています。

擬似乱数生成エンジンは代表的なものとして、メルセンヌ・ツイスター法、線形合同法、キャリー付き減算法というものがあります。

今回は、長周期の乱数列を高速に生成できることで優秀な、メルセンヌ・ツイスター法を用いて乱数を生成していきます。

正規分布生成器を初期化する

double mu = 0.0, sig = 1.0;
std::normal_distribution<> dist(mu, sig);

この部分で平均mu、標準偏差sigを引数にとる正規分布生成器の初期化をおこなっています。

移動ロボットの分野ではよく平均と分散という言葉を用いますが、今回のdistの引数は分散ではなく平均ですので注意が必要です。

（分散 = 標準偏差^2）

生成した乱数の分布を確認する

残りの部分ではxの値を小領域に区切って、その範囲に存在している乱数の個数を数えています。
結果の描画にはmatplotlibを使用しています。

matplotlibはpythonのライブラリですが、なんとc++でも使用することができるんです。
以下の記事も参考にしてみてください。

c++でmatplotlibを使う | MY ROBOTICS

また、この正規分布に従う乱数はc++11以降のバージョンでの実装となりますので、コンパイルするときは以下のようにc++11のオプションをつけるのをお忘れなく。

-std=c++11

実行結果

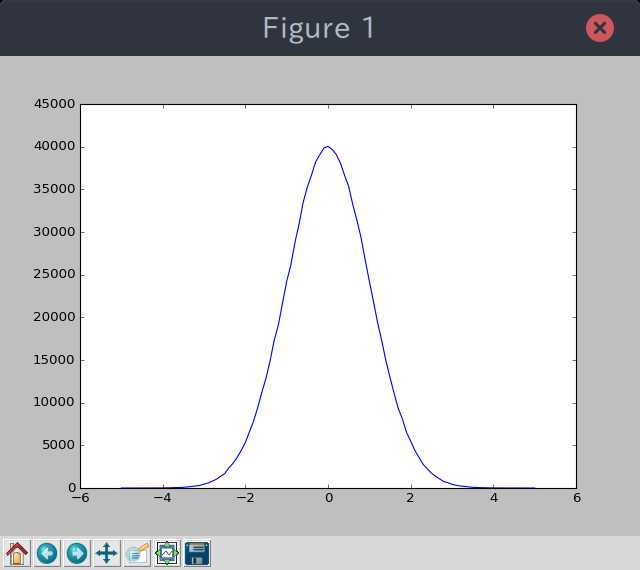
実行すると、こんな感じになります。
ちゃんと正規分布になっていることが確認できました。