Blackjackベーシックストラテジーの控除率を求める
人生で初めてカジノに行く機会があり、ブラックジャックをプレイ。
20ドル勝ちました。笑
ところで皆さん、ブラックジャックというゲームにはベーシックストラテジーという自分の手札がこの時はこうする。
という行動指針があることはご存知でしょうか。
このベーシックストラテジーに乗っ取ってプレーすると、控除率はわずか0.5%ほどになるそうです。
この控除率がカジノの利益になるわけです。
つまり、1ゲームあたり1000円を賭けた場合、平均的な期待値は995円となるわけです。
日本の宝くじなんかは控除率が50%近いことを考えると、ものすごいことですね。
今回はこのベーシックストラテジーに乗っ取って行動した場合、控除率が何%になるのかをブラックジャックのプログラムを組んで検証してみたいと思います。
ブラックジャックのルール
先ほど、控除率はわずか0.5%程になると記述しました。
実はブラックジャックには細かなルールがいくつか存在していて、カジノによって適用されるルールがまちまちなのです。
そこで、今回検証するブラックジャックのルールは、私が経験したカジノでのルールに乗っ取って、以下のようにします。
- 6デッキ
- ディーラーは16以下でヒット、17以上はスタンド
- ブラックジャックの払い戻しは3/2倍
- サレンダー不可
- スプリット後のダブルダウン可能
ベーシックストラテジー
今回使用するベーシックストラテジー表はこれ。
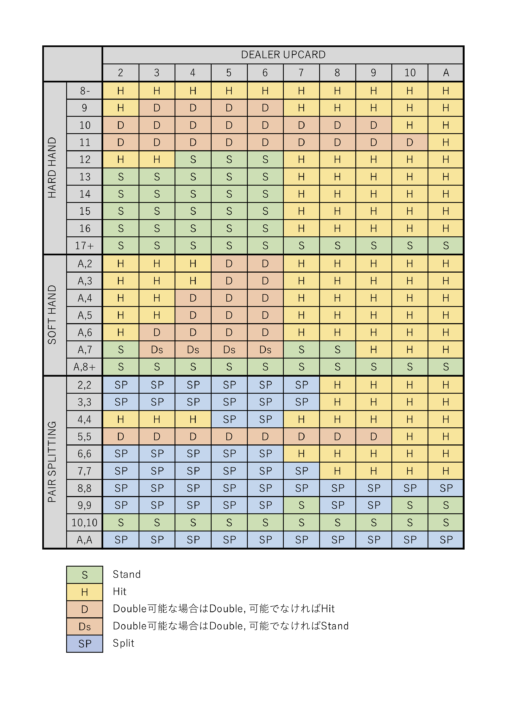
今回はサレンダー不可での実装となっているので、ソフトハンドのA,6 , A,7の部分は全てヒットとなっている。
このようなベーシックストラテジーの表は、ググれば色々ヒットする。
この表をコードに起こすのが地味に面倒臭かった。。。
ブラックジャックの実装
先ほどのルールに乗っ取ったブラックジャックをC++で実装する。
すぐできるだろうと思って始めたものの、想像以上に行数が多くなってしまった。
面倒臭いので、このコードの解説とかはしません。はい。
コードはgitに上げてありますので、そちらを参考にしてみてください。
https://github.com/myrobo/blackjack
実装は、、、多分合っているはず。はず。はず。
間違いがあったら指摘して欲しいです。( About me … のページ下部のコメントにてお願いします。)
調子に乗って、インシュランスやBET金額を毎回変更できるような実装にしてしまいました。
ルールの変更(サレンダーの有無の変更)も実装してみました。
暇があったら、カウンティングの戦略を研究するのも面白いかなと思います。
簡単な仕組みで還元率が100%を超えるような戦略を見つけてみたいものです。
今回の検証では、BET金額は毎回1(単位コイン)。
インシュランスは基本的に損をする仕組みですので、行いません。
検証1 surrender無
試しに、ディーラに対して5人のプレーヤーをつけ、それぞれベーシックストラテジーで戦ってもらいます。
5人のプレーヤーはインシュランスは行わず、BET金額は毎回1としてあります。
ゲーム回数は10万回とします。
int main() {
int buttles = 100000;
bool can_surrender = false;
Player player1( std::string("player1"), bet_strategy, insurance_strategy, basic_strategy );
Player player2( std::string("player2"), bet_strategy, insurance_strategy, basic_strategy );
Player player3( std::string("player3"), bet_strategy, insurance_strategy, basic_strategy );
Player player4( std::string("player4"), bet_strategy, insurance_strategy, basic_strategy );
Player player5( std::string("player5"), bet_strategy, insurance_strategy, basic_strategy );
std::vector<Player> player_list{ player1, player2, player3, player4, player5 };
Dealer dealer( player_list, can_surrender, buttles );
dealer.execute();
dealer.show_result();
return 0;
}10万回の勝負の結果は、、、
| Player1 | Player2 | Player3 | Player4 | Player5 | |
| Coin | -1159 | -1311.5 | -844.5 | -1291.5 | -1134 |
| 還元率 | 98.841% | 98.6885% | 99.1555% | 98.7085% | 98.866% |
Player3が勝負強いですね。健闘しています。
控除率は1%程でしょうか。
どこかのでブラックジャックの控除率は0.5%程っていう記事を見かけたのですが、、、
ルールの違いってのもあると思います。
それとも私の実装ミス?
これほど還元率の高いゲームはブラックジャック以外ないでしょう。
実際私が行ったカジノでも、ブラックジャックのテーブルが一番多く、一番賑わっていました。
検証2 surrender有
では、surrender有のルールに変更すると、どれほどPlayerが有利となるのでしょう。
今回も5人のプレーヤーに10万回勝負をしてもらいます。
int main() {
int buttles = 100000;
bool can_surrender = true; // <- ここを変更すると、surrenderのルールを変更できる
Player player1( std::string("player1"), bet_strategy, insurance_strategy, basic_strategy );
Player player2( std::string("player2"), bet_strategy, insurance_strategy, basic_strategy );
Player player3( std::string("player3"), bet_strategy, insurance_strategy, basic_strategy );
Player player4( std::string("player4"), bet_strategy, insurance_strategy, basic_strategy );
Player player5( std::string("player5"), bet_strategy, insurance_strategy, basic_strategy );
std::vector<Player> player_list{ player1, player2, player3, player4, player5 };
Dealer dealer( player_list, can_surrender, buttles );
dealer.execute();
dealer.show_result();
return 0;
}10万回の勝負の結果は、、、
| Player1 | Player2 | Player3 | Player4 | Player5 | |
| Coin | -1113.5 | -942.5 | -1168.5 | -336 | -839.5 |
| 還元率 | 98.8865% | 99.0575% | 98.8315% | 99.664% | 99.1605% |
Player4が大健闘。
やはりサレンダーのルールが加わったことによって、少しPlayer側が有利になりました。
検証3 surrender有 & 常にinsurance
冒頭で、インシュランスは損をする。と書きました。
insuranceできる時は常にinsuranceをかけるようにすると、どれほど還元率に影響がでるのでしょう。
これも先ほどと同様に10万回勝負を行います。
bool insurance_strategy( std::vector<int>& deck ) {
return true; // <-ここを変えます
}10万回の勝負の結果は、、、
| Player1 | Player2 | Player3 | Player4 | Player5 | |
| Coin | -4142.5 | -3922.5 | -3352.5 | -3782 | -3591 |
| 還元率 | 95.8575% | 96.078% | 96.6475% | 96.218% | 96.409% |
やはり、インシュランスは損をすることがわかります。
それもそのはず。
山札に均等にカードが入っているとすると、その中から10(10,J,Q,K)を引く確率は、4/13。
それに対してインシュランスで勝った場合は3倍の配当。
インシュランスの還元率は、
4/13 * 3 = 12/13 ( < 1 )
1を下回っています。そういうことですね。
結論
やはり確率論者の観点からすると、還元率が100%を超えない限りブラックジャックで長時間遊ぶ気にはなれません。
こうなると、意地でも還元率100%を超えるカウンティングの方法を探してみたいですね。
暇があれば考えてみたいと思います。
それにしてもこのブラックジャックのルールはよく考えられていると思います。
還元率100%の少し下のギリギリのラインを狙ってきているのですから。感心です。
皆さんも勝ち逃げのタイミングを逃さないようにしてくださいね。
ではでは。