少し真面目な話をしたくなったので、LiDARの計測モデルについて記述していこうと思います。

ここで取り扱う話は主に、移動ロボットの自己位置推定として広く用いられているLiDARについてです。この記事を通してみなさんの理解が少しでも深まれば幸いです。

LiDARで物体との距離を測る際の誤差

まず、LiDARから出る1本のレーザで物体との距離を測ることを考えます。

例えば、LiDARから計測する物体までの距離がちょうど10mだったとします。この状態でLiDARを用いて物体との距離を10回計測すると、結果はどうでしょうか。10回の計測が全て10mピッタリ。ということは決してありません。10.012m、9.985m、10.007m、9.992m、・・・という具合に10mを中心に多少のばらつきが生じることは容易に想像がつくと思います。

10.003mとか、9.994mあたりの比較的10mに近い数値はたくさん出ると思います。では、10.103mとか、9.875mの数値はどうでしょうか。±10cm。頻繁には出なさそうですが、ひょっとしたら10回に1回ぐらいは出るかも。といったところでしょうか。では、10.236mは？、、、

以上の質問からもわかるよう、LiDARでは（LiDARに限らず、多くの計測機器では）真値に近い値は頻出しますが、真値から離れるにつれてその頻度は少なくなると考えられます。

ロボットの世界では、このような誤差はしばしば正規分布として近似されます。

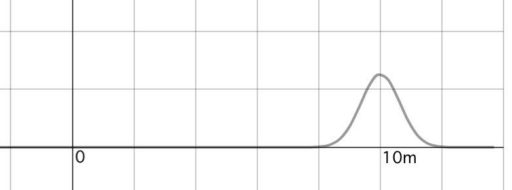
ここで正規分布について詳しくは触れませんので、詳しく知りたい方は各自調べましょう。

移動ロボットにて環境を認識する

今時刻 t において、ロボットは地図 m を持っており、姿勢が x_t であるとしましょう。

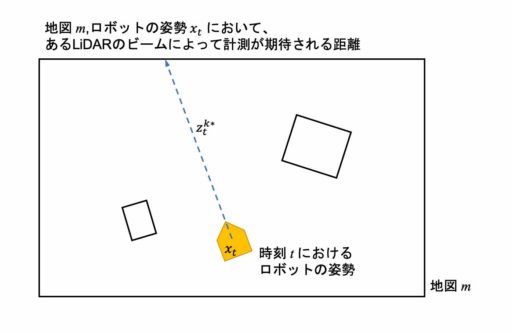
ここではまず。複数あるLiDARのビームのうち正面のビームに絞って考えます。あるLiDARのビームによって計測が期待される距離 z_t^k の添字 k は、複数あるLiDARのビームのうち（移動ロボットで使われるLiDARの多くは中心から放射状に複数方向の距離が取得できる）k番目のもの。という意味になります。

このような状況でロボットが正面のLiDARのビームを用いて距離を計測した場合、その計測値の分布はどのようになるでしょうか。

LiDARの4つの計測モデル

冒頭で、真値とのズレを正規分布で近似するということを述べましたが、例えば、LiDARの前を人が横切ったらどうなるでしょうか。その場合、期待していた測定値よりも遥かに短い値をLiDARは観測することになるでしょう。

移動ロボットで周囲環境を認識する際には、歩行者や車などの地図には記載されていない障害物により、期待される値（地図と現在の姿勢から期待される測定距離）から大きく外れた値が観測されることがあります。

LiDARでいかに示す4つの場合についてそれぞれモデルを考え、それらを最終的に混ぜ合わせることで1つの計測モデルとして扱うことが多いです。

• 地図に記述されている物体を正しく計測した場合
• 地図に記載されていない想定外の物体により実際より短い距離を検出した場合
• 計測に失敗した場合
• 原因不明のでたらめな計測

これらについてそれぞれどのようにモデリングすれば良いでしょうか。それぞれのモデルについて以下で詳しく見ていきます。

1. 地図上の物体を正しく計測する確率

まずはじめに、地図上の物体を正しく計測する確率の確率分布をモデル化します。これは冒頭でもお話ししたように、正規分布（ガウス分布）に基づく分布としてモデル化されます。時刻 t において地図 m、自己位置 x_t が与えられた時、k 番目のビームが距離 z_t^k を観測する確率の分布を

$$p_{hit}( z_t^k | x_t, m )$$

とします。地図上の障害物に正しくレーザが照射（hit）される確率 p 。
これは正規分布となるので、グラフで表すと以下のようになります。

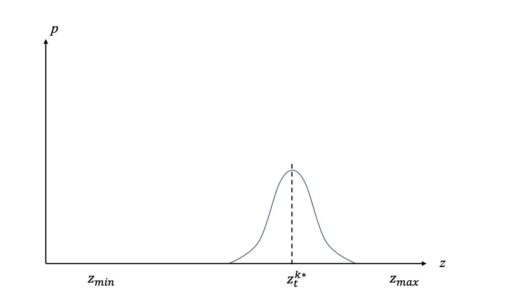
ここで、LiDARは計測できる範囲が限られていることに注意が必要です。LiDARは極度の近距離は正しく計測が行われないことが多く、また、性能により計測できる最大距離が決まっています。そこで、LiDARの測定可能距離の上限下限を

$$z_{min}, z_{max}$$

とし、分布はその範囲内に限るものとしています。この特性は以下2~4の計測モデルにも同様に当てはまります。

2. 地図上にはない物体を計測する確率

次に、地図には記載されていない物体（例えば人や車などの移動障害物）を計測する確率をモデル化します。

移動物体がLiDARのビームを遮る時は、常に期待される観測値よりも小さい値を検出します。
例えば、地図上で壁までの距離が10mだった時、移動障害物が壁とLiDARとの間に存在すれば、検出距離は5mや6mというように、10mよりも小さい値となります。（壁の向こう側に移動障害物が存在しても、検出は12mとはなりませんね。その場合、レーザは壁で跳ね返るため。）

また、地図には記載されていない物体を計測する可能性は、距離とともに減衰します。
例えば、片側1車線の通りを車が絶え間なく行き交っています。歩道から車を眺めた時、手前の車線を走る車と、奥の車線を走る車、どちらの方がよく見えますか？当然手前ですよね。
LiDARも同じで、奥のものを観測しようと思ったら、その物体より手前が空いている必要があります。この理由から、観測距離が遠ざかるにつれて、観測確率も減衰します。これは数学的には指数関数で表されます。

この地図にはない物体を観測する確率の分布は、

$$p_{short}( z_t^k | x_t, m )$$

とします。地図上の障害物の距離よりも短い距離（short）を観測する確率 p 。
その分布は、グラフで以下のように表されます。

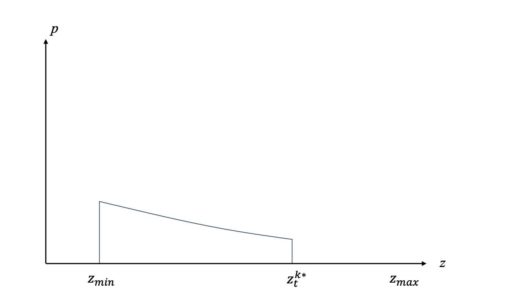
3. 計測を失敗する確率

LiDARはまれに計測を失敗することがあります。（例えば、北洋電機製のLiDARをROSで動かした場合、計測データにNaNが入ることがあります。これは何らかの理由で計測が失敗したことを意味します。）

このように、計測失敗をNaNのように数値意外の値でお知らせしてくれるLiDARは親切なのですが、場合によっては、LiDARの計測可能距離の最大距離を出力するものもあるそうです。（この分野で有名な学術書「確率ロボティクス」にも、最大距離を出力する場合を取り上げていますので、それに習いここでも計測失敗時に最大距離を出力するものとして、計測失敗確率のモデリングをしようと思います。）

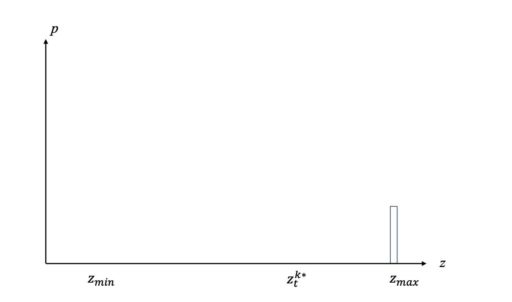
計測を失敗する際の確率の分布は、

$$p_{max}( z_t^k | x_t, m )$$

とします。計測失敗、つまりLiDARが計測可能距離の最大値（max）を観測する確率 p 。
その分布は、グラフで以下のように表されます。

4. でたらめな計測を行う確率

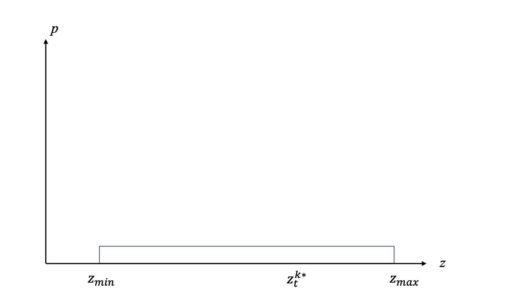
最後に、LiDARは時々、完全に説明のつかない計測値を出力することがあります。これらは、LiDARが検出しうる範囲て一定の確率で分布しているものとします。その確率分布は、

$$p_{rand}( z_t^k | x_t, m  )$$

で表します。完全にでたらめ（rand）な値を観測する確率 p 。
この分布は、グラフで以下のように表すことができます。

観測確率の混合

以上4つの観測確率が全て合わさることで、1つのLiDARビームの観測確率となります。これらの観測確率は重み付きで混合されます。最終的な、時刻 t において地図 m、自己位置 x_t が与えられた時、k 番目のビームが距離 z_t^k を観測する確率 p は、それぞれの重み係数を

$$z_{hit}, z_{short}, z_{max}, z_{rand}$$

として、

$$p( z_t^k | x_t, m )=\begin{pmatrix} z_{hit} \\ z_{short} \\ z_{max} \\ z_{rand} \end{pmatrix}^T \begin{pmatrix} p_{hit}( z_t^k | x_t, m ) \\ p_{short}( z_t^k | x_t, m ) \\ p_{max}( z_t^k | x_t, m ) \\ p_{rand}( z_t^k | x_t, m ) \end{pmatrix}$$

と表すことができます。当然確率なので、分布の合計は1とならなければなりませんので、それぞれの係数の和について、

$$z_{hit} + z_{short} + z_{max} + z_{rand} = 1$$

となります。
この、混合後の確率分布をグラフで表すと、次のようになります。

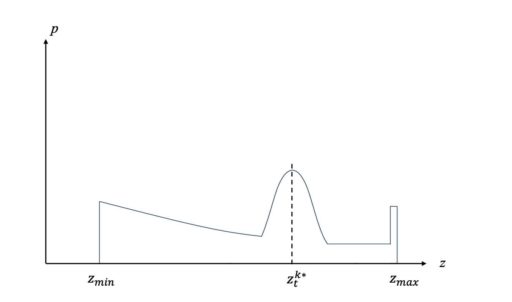
この確率分布は、LiDARのある1本のレーザについてですので、自己位置推定の際には、最終的には全部のレーザについて観測確率をもとめ、それらの確率を掛け合わせることにて尤度を求めることになります。

実用例としては、ROSのナビゲーションスタックにて、amcl（パーティクルフィルタによる自己位置推定）でも取り入れられていたと思います。z_hit, z_shortなどのパラメータをドキュメントで見かけたことがあるのではないでしょうか。

例えば、カメラなどを元に周囲の混雑状況を把握し、これらのパラメータを動的に変更する自己位置推定なんてものがあったら面白いのではないでしょうか。（人混みが多ければ、z_shortの重みを大きくするとか。）

LiDARの観測モデルについて、大まかな説明していきました。皆さんの理解が少しても深まれば幸いです。お付き合いありがとうございました。