二次関数のグラフの書き方

このページでは、高校数学で扱う二次関数のグラフの書き方を１から分かりやすく解説していきます。
グラフを書くに当たって躓きやすい頂点の求め方や平方完成の仕方など、図を交えながら丁寧に解説していきます。
数学の苦手な方でもコツさえ掴んでしまえば、簡単に二次関数の問題を解くことができますので、頑張っていきましょう。

まず初めに、二次関数の基本中の基本、 y = x² のグラフの形をマスターしましょう。

初めに、関数 y = x² がどの点を通るか調べてみます。
たとえば、 x = 0 の時、 y = 0 となります。 また、 x = 1 の時は、 y = 1 となります。
このように、いくつかのxの値について調べて見ると、 ( -2, 4 ) ( -1, 1 ) ( 0, 0 ) ( 1, 1 ) ( 2, 4 )
この関数はこのような点を通ることがわかります。

これらの点をグラフにプロットしてみましょう。

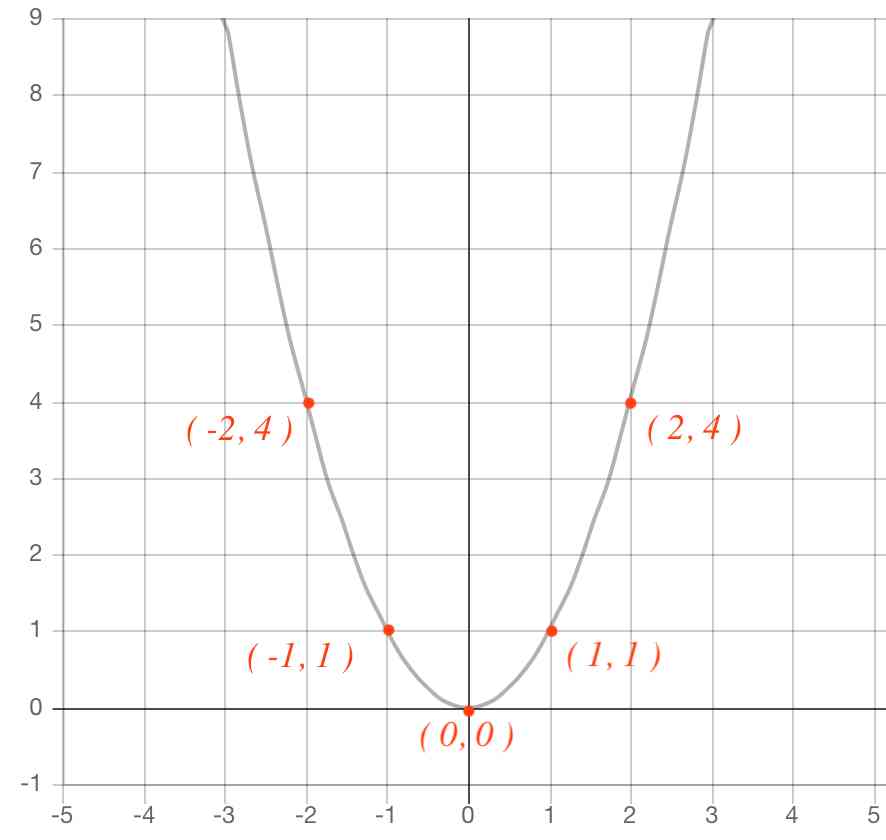
これらの代表的な5点をグラフにプロットすると、その関数が通るであろう大まかな位置を知ることができます。
これらの点を滑らかにつなぎ合わせると、このような山形なグラフとなります。

二次関数のグラフは山の尖り具合や向きは違えど、すべてこのような形状となります。
物を投げた時に、このような形状を書きながら飛んでいくことから、二次関数のこのような形状は放物線と呼ばれます。

次に、先ほとの基本の二次関数 y = x² を発展させて、 y = ax² のグラフについて考えてみましょう。

この変数 a は、二次関数のグラフの尖り具合を表しています。
先ほどの基本形では、 a = 1 の時について考えていたことになりますね。

では、この係数 a aを変化させるとどのようにグラフの形状が変化するでしょうか。
例として、 a = 2 、 a = 0.5 、 a = -1 の時のグラフをみてみましょう。

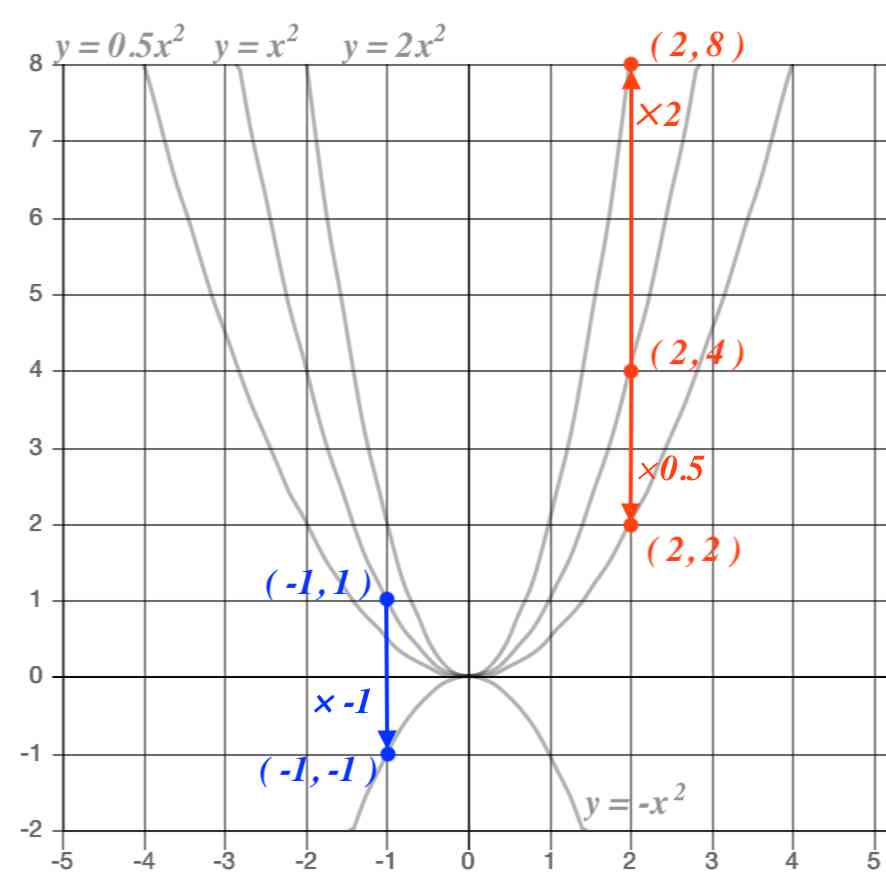
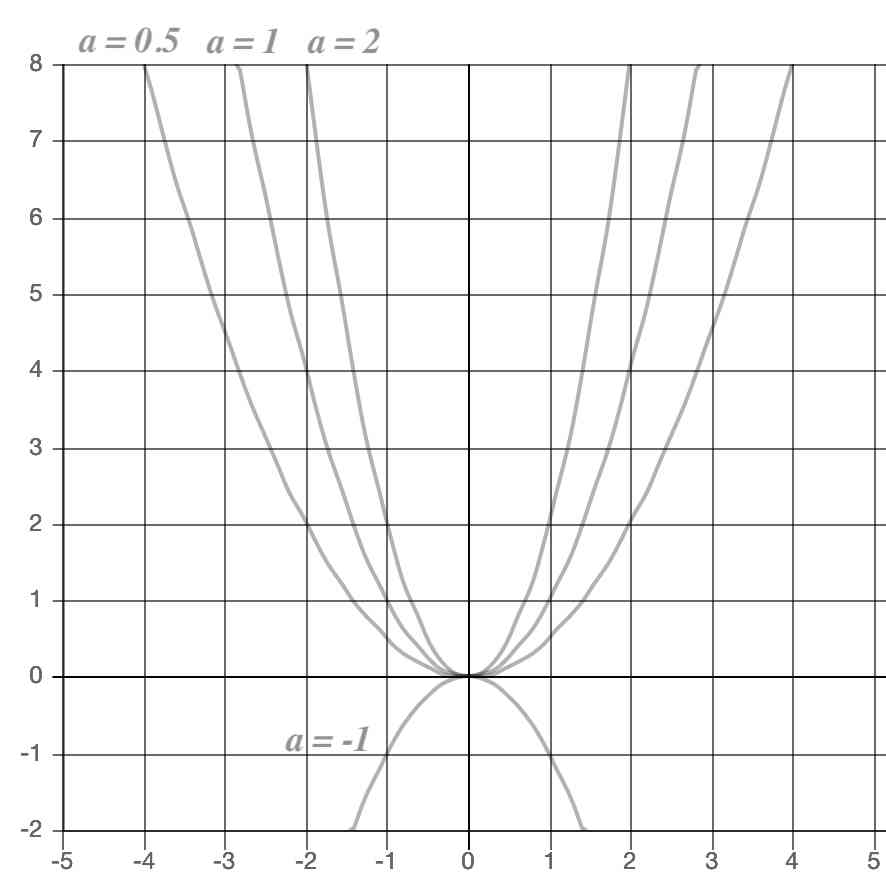
このように、係数 a の値が大きくなるほどグラフの尖り具合は鋭くなります。
a = 0.5 の時のように係数の値が0に近づくほど、グラフの尖り具合は緩やかになります。
また係数がマイナスの場合は、グラフの山が反転して上に尖った形となります。

係数 a の値が正で、下向きに尖っているグラフを 下に凸
係数 a の値が負で、上向きに尖っているグラフを 上に凸

と言います。

今度は、先ほどの関数 y = ax² をさらに発展させ、グラフをy軸方向に平行移動させてみます。

例として、 y = x² のグラフを y = x² + 2 に変更してみましょう。

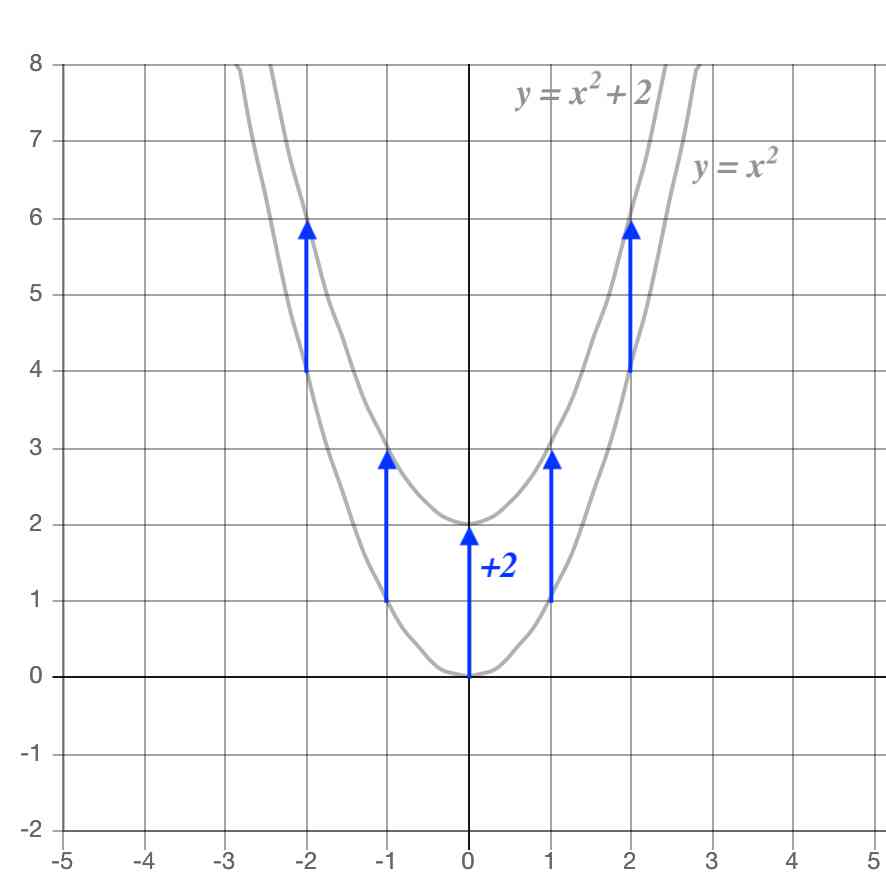
図からもわかるように、 y = x² + 2 のグラフは y = x² をy軸方向に平行移動することを表します。

このように、 y = ax² + q の係数 q は y軸方向への並行移動量を示します 。

今度は先ほどの関数を、さらにx軸方向に平行移動させてみます。
先ほどの関数 y = x² + q の x の部分を、 ( x - p ) に変更すると

y = a( x - p )² + q のような関数となります。

例として、ひとつ前のセクションで使用した y = x² + 2 にさらに手を加え、
y = ( x - 1 )² + 2 としてみましょう。

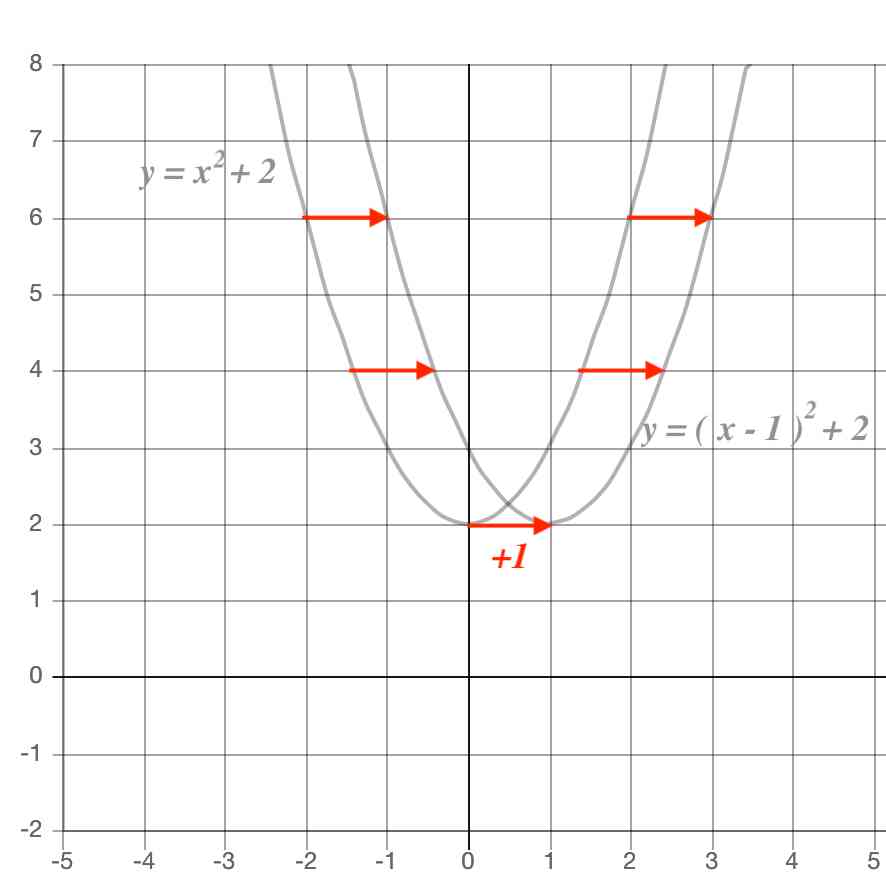
図からもわかるよう、 x を ( x - 1 ) で置き換えることは、グラフをx軸方向に 1 だけ並行移動することを意味します。

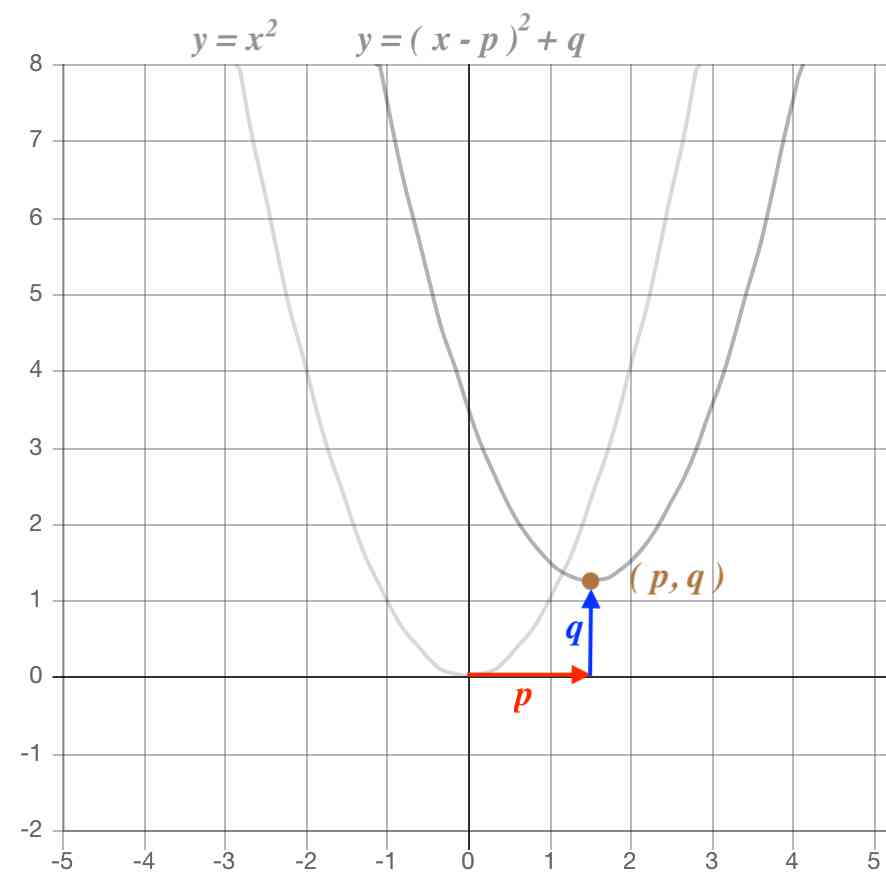
以上から、 y = a( x - p )² + q のグラフは y = ax² のグラフを

x軸方向に p
y軸方向に q

平行移動させる ことを意味します。

これで、 y = a( x - p )² + q の形をした関数のグラフを書くことができるようになりましたね。

先ほどまでで、 y = a( x - p )² + q のグラフを書くことができるようになりました。

しかし、教科書や問題集で見かける二次関数の多くは、 y = ax² + bx + c のような形をしていると思います。
このような関数のグラフを書くにはどのようにすれば良いでしょうか。

このような関数の場合は、 平方完成 により y = a( x - p )² + q の形に式変形することでグラフの頂点の位置を求めていきます。

y = a( x - p )² + q の形をした関数を y = ax² + bx + c の形に式変形する方法を、順を追ってみていきましょう。

ここでは、関数 y = 2x² - 4x - 1 を例として、平方完成によりグラフの頂点を求めていきます。

1. 係数aでくくり出す

2. 平方完成ができるよう、カッコ内の定数を調整する

3. 平方完成に必要のないものを、カッコの外に出す

4. 平方完成

5. 平方完成後の関数の形から、グラフの頂点・尖り具合を求める

6. 実際にグラフを書いてみる

ここまで式変形ができたなら、実際にグラフを書いてみましょう。
先ほと求めた二次関数の頂点の座標をまずグラフにプロットします。
次に、二次関数の係数aが正であることからグラフは下に凸なグラフとなりますので、頂点を基準に滑らかに下に凸な放物線を書きましょう。

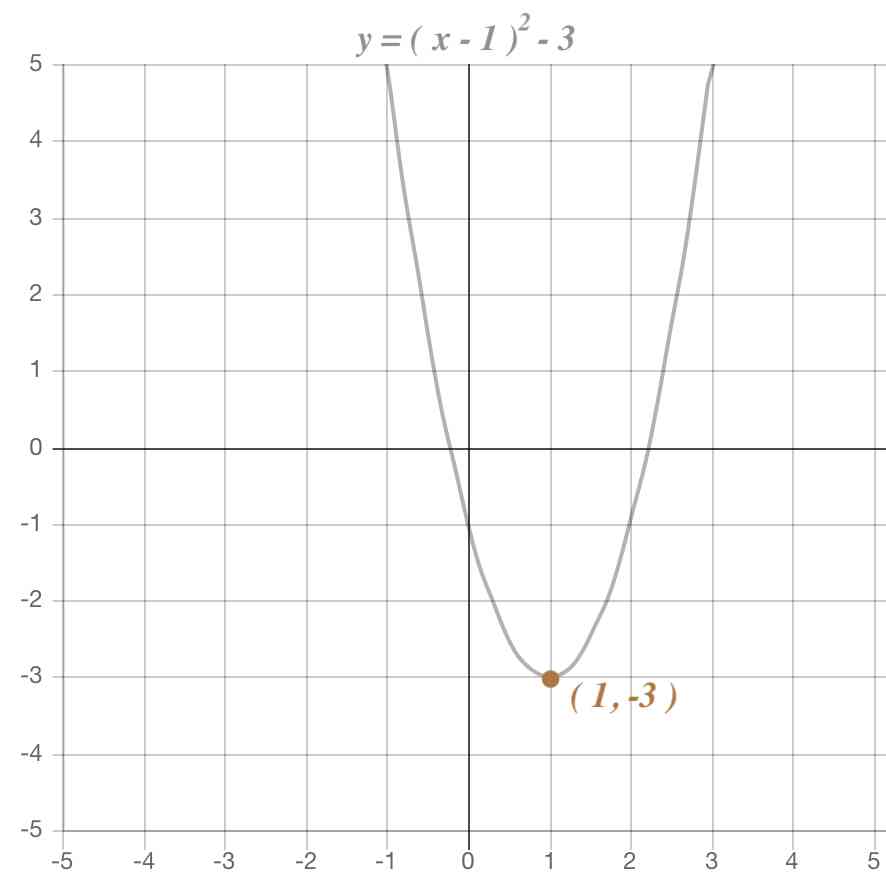
不安な方は、頂点以外にも何点か通る場所を調べ、その点を通るような滑らかな曲線を書くことでより正確なグラフを書くことができます。
関数の尖り具合に関しては、以下のものを参考にしてみると良いかと思います。

正しく書けましたか？
本サイトのメインページでグラフの概形をチェックしてみましょう。